Introduction

test The overall computer industry has changed drastically in the last 5-10 years. With multicore computing we no longer see the pattern of single chips with increasing clock speeds being released, we see the number of cores on a given chip increase as time goes on. In spite of this, Moore's law persists which lets us expect machines with hundreds if not thousands of individual cores in the not so distant future. Because of this we can also expect the physical makeup of individual machines to vary significantly and possibly be made up of heterogeneous smaller computational components. As described in the Berkeley View [2] this poses an enormous problem to the performance portability of code, as performance and portability are classically conflicting objectives when it comes to software generation. This is obviously a major concern in distributed computing as well since it is essential to have efficient code throughout the system, regardless of what physical architecture it resides on. For this reason, having code that can 'auto-tune' itself to achieve near optimal performance on any given hardware architecture will be a key issue moving forward within the distributed computing community and will be absolutely essential if the dream of a true distributed operating system running at internet scale is ever to be realized.

Many problems within the world of linear algebra have auto-tuned libraries which achieve near-optimal performance on a wide range of machines. One such system is ATLAS [9], which is presented here as an example. The problem with these libraries are that they are not general enough to service all of the high performance computing needs of the scientific community and the optimizations they employ are too specific to be applied to other problems. To combat this, a new area of general purpose frameworks for performance-portable code is emerging. The purpose of this literature review is to give the reader an overview of the most popular such frameworks that exist today, give an idea of how they work and briefly discuss their overall performance.

Motivation

The main motivation behind this work was presented in the The Landscape of Parallel Computing Research: A View from Berkeley [2]. This document discusses the recent switch of the computer hardware world to multicore processors and the drastic changes that need to be implemented in the software world to be able to adapt to the next generation of computers. The scope of this paper is much more than can be covered here, so the only important aspects that motivate our later discussion will be looked at.

Moore's law describes a trend in computer hardware where the number of transistors that could affordably be put on a chip doubled every 18 months to two years. In terms of processors, this would mean that one could expect faster and faster sequential computers to come out on a regular basis. This lead to the conventional wisdom that there was no real need for major optimizations or to parallelize sequential programs because they would simply run faster once a new generation of processors came out. However, due to many factors, the performance of individual processors have not been meeting the exponential improvements that they have in the past. In spite of this, Moore's law persists. Instead of seeing faster and faster individual cores, we now see the number of processor cores on a chip going up. It is currently not uncommon for a personal computer to have 2, 4 or even 8 processor cores. As this trend continues we can expect chips with thousands of individual cores on a single chip in the not so distant future. On top of this, it is not hard to imagine that the physical makeup of individual machines will vary significantly and possibly be made up of heterogeneous smaller computational components as well.

This obviously introduces some major problems into the world of computer software. Software vendors can no longer rely on faster individual cores to improve the performance of their sequential programs. Many already parallelized programs will not be able to scale as the number of cores increase dramatically, meaning they will effectively reach a performance barrier as well. Another equally, if not more urgent, problem is the issue of code performance portability. Currently, we write code and compile it to be efficient on a given machine. When this code needs to be run on a different machine, it is possible that significant changes must be made to the code and compilation process to get near optimal performance. Obviously this is undesirable as it demands a significant amount of time to adjust and tune the code by hand by highly trained experts. As the variety and complexity of heterogeneous systems increase, the time needed to hand tune code for specific machines becomes unmanageable. This is a key concern within distributed systems as overall performance is largely influenced by how quickly individual machines can execute code. If only a small number of machines have optimal code, then either the operating system will always try to use these machines for specific tasks, or it will run the tasks on machines with suboptimal implementations of the given code. Either way this results in poor overall performance.

One potential solution to these problems are new programming models and auto-tuning frameworks. Programming models need to allow the programmer to balance their productivity with implementation efficiently. One key way to do this is to abstract the underlying architecture from the programmer. This will allow the programmer to worry about implementing their program and leave the low level details to the system. However, regardless of the programming model used, the overall performance will be determined by the quality of the generated code, which is currently done by the compiler. The compiler is responsible for the optimization selection and then choosing the parameters for these optimizations as well as choosing between different alternative implementations of library kernels. This search space is often too large for a compiler to be able to make all of the right choices all of the time on every different computer architecture. Also, it is very difficult to add new optimizations into existing compilers and is often not worth the time needed to implement them. Because of this, most optimal solutions have to be manually tuned for each different system, taking a significant human investment. This is where auto-tuners step in. An auto-tuned algorithm is one that effectively searches through the optimization search space (either at compile time or run time) to produce efficient implementations on a wide array of hardware architectures. Auto-tuners have become popular in the last few years to produce highly portable, efficient scientific code. Many of these auto-tuners do this by generating many different algorithm variations of a given problem and then benchmark each one on a specific machine. The search also tries many combinations of the optimizations available through the compiler. This is a lengthy process, sometimes lasting several hours, but it only needs to be performed once at install time. The resulting implementation is often significantly faster than a naive implementations and sometimes even produces code faster than vendor supplied libraries. This is accomplished because the auto-tuner searches the optimization space in ways that a person would not, often finding unusual and unexpected optimization combinations. In the next section, an example of an auto-tuner implementing linear algebra libraries will be presented.

An Example of an Auto-tuned Algorithm: ATLAS

ATLAS (Automatically Tuned Linear Algebra Software) [9] is a software package that was produced to provide a portable and efficient implementation of the Basic Linear Algebra Subprograms (BLAS), a widely used linear algebra library. ATLAS is regarded as some of the earlier pioneering work in the field of auto-tuning algorithms, still being used by the scientific community as well as other researchers as a performance benchmark today.

BLAS are building block methods for performing basic linear vector and matrix operations. It has three logical levels. Below these levels are described as well as a brief summary of what ATLAS tries to do to make their code more efficient at each level.

Level 1 BLAS

This level performs vector-vector operations. At this level it is not possible to process the vectors to be able to reuse memory (as it is with matrix operations), and is expected to only achieve a roughly 0-15% speedup over untuned code. Generally the compiled can do a good job of optimizing this code so not many extra optimizations are performed by ATLAS.

Level 2 BLAS

This level performs matrix-vector operations. At this level using appropriate cache and register blocking can drastically reduce the references that must be satisfied out of main memory. By ensuring that certain segments of vectors and matrices remain in registers or in cache for a significant amount of time, one can expect a modest 10-300% speedup at this level.

Level 3 BLAS

This level performs matrix-matrix operations. Using major-block format for the matrices (with the correct size blocks) allows for a minimization of cache thrashing as well as maximizing the amount of cache that gets reused. Another important aspect of these operations is deciding on the order in which the matrices are computed in, especially if you are dealing with relatively small matrices. If not, a relatively complex partitioning of the matrices can ensure maximum memory reuse, which will in-turn produce significant performance improvements. A lot of significant details are being omitted here, but suffice to say that ATLAS achieves orders of magnitude of speedup at this level.

At install time ATLAS runs a series of benchmarks to calculate the various cache and main memory sizes as well as to determine various latency timings within the given system. ATLAS also probes the system to gain information regarding the floating point units of the system. On top of this, ATLAS explores other optimizations such as loop unrollings and blocking factors and applies the best ones found.

Although many of the details of ATLAS have been omitted here, it is hoped that this gives the reader an idea of what an auto-tuned algorithm tries to accomplish. Auto-tuning algorithms have been very successfully in the area of linear algebra (see [3, 4, 7] for other examples), however little has been done on non-numerical problems. One potential reason for this is the investment it takes to produce an efficient, portable auto-tuned algorithm. ATLAS and systems like it are certainly not trivial and are the result of many years of research and development. Another issue is that many other problems do not have the regular and pre-known data qualities that are common to many linear algebra problems. It is for these reasons that recently more general purpose approaches have taken off.

General Purpose Frameworks for Performance-Portable Code

As stated in the previous section, there has been a significant amount of work put in to auto-tuning algorithms related to linear algebra problems but not much work done outside of this. To combat this, some researchers looked at the problem of portable performance from another angle. Instead of focusing on a single problem and building an auto-tuned algorithm to solve that problem efficiently on a wide variety of computer architectures, we are starting to see the emergence of general purpose frameworks for performance-portable code. Generally speaking, these frameworks allow the programmer to define the problem that they are trying to solve without explicitly worrying about specific performance details. The framework would then have some kind of auto-tuner to then tune the code to allow for an efficient implementation on a given machine. Although this area is relatively small, there are already a handful of very powerful frameworks that allow for performance-portable code. In the following subsections an overview of the available frameworks will be given.

ADAPT

ADAPT [8] represents one of the earlier general purpose frameworks we will look at. It was realized that with the convergence of modern computing technology that it was possible to produce a single executable program for a wide range of compatible but still wildly varied computer systems. These differences can come from different memory sizes and hierarchies, processors and networking capabilities, all of which can have a significant impact on performance if not taken into consideration by the running program. To overcome this issue, Voss et. al proposed APAPT, a system that supports dynamic code compilation with parameterization while allowing the user to search the the optimization space to achieve near optimal performance.

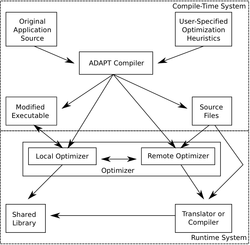
ADAPT has two main components, one being compile-time and the other being a run-time component. ADAPT provides its own language (ADAPT Language, or AL for short) for the users to define their optimization heuristics to be applied by the ADAPT run-time system. An example of an optimization heuristic written in AL was given in the paper, and it was for a dynamic loop unroller. Using this language it is possible to code a very wide range of optimization heuristics to help optimize the application code. The ADAPT compiler reads the application code as well as user-defined optimization heuristics and generates a run-time system for applying these these heuristics dynamically to the application. To do this, the compiler first identifies code pieces that are candidates for optimization. The compiler then generates a run-time system based on the candidate code sections as well as the user supplied optimization heuristics. This run-time system consists of the original application code with new control paths for each optimization candidate. For each candidate, the first path represents the best known version of the code (using whatever optimizations have been applied in the past) and the second path represents an experimental version. Every time a new experimental version is created, it is run at the next opportunity (the next time that piece of code is called). The experimental version is monitored and then its performance data is fed back into the optimizer. This allows the ADAPT optimizer to successively swap in better and better performing pieces of code and represents a key component of the overall ADAPT framework.

The ADAPT optimizer consists of two parts, a local optimizer as well as a remote optimizer. The local optimizer identifies hotspots within the code, representing the most time consuming sections. The local optimizer will then communicate this information to the remote optimizer which has the source code of each candidate, a description of the target machine, the user specified optimization heuristics and tools and compilers that can be used to optimize the code. The remote optimizer then optimizes the code with all of the tools it has available to it and when a new code variant is produced, it is sent back to the local optimizer to be dynamically linked into the running application to be run and evaluated at the next opportunity. The more that a section candidate code is run, the faster it gets over time due to this process. ADAPT relies on this fact to achieve peak performance in its applications. An overview of the ADAPT framework can be seen provided figure.

The ADAPT framework was then tested on two different computer systems by running six different experiments. These experiments covered different applications, including floating point benchmarks, kernels for matrix-matrix multiplication and a finite differencing solver. These experiments give an idea of the variety of techniques that can be implemented using the ADAPT framework. It was found that, on average, the ADAPT system offers a better solution than static optimization tools. In general, ADAPT was found to offer the best performance with the least risk of degradation in all of the tests performed.

STAPL

Thomas et. al introduced a general framework for adaptive algorithm selection called the Standard Template Adaptive Parallel Library (STAPL) [5]. They realized that often times there are many algorithms that can solve a problem, all of which perform differently depending on many factors and deciding which one to use was often a difficult problem. This problem only gets worse in distributed settings. These issues are direct contributors to the problem that we have been trying to address in this paper, the problem of writing portable code that performs well on a variety of hardware architectures and for various input sizes. Thomas et. al thought that the programmer should only indicate which operation to be performed and it should be up to the system to decide which algorithm to use. The main focus of STAPL is on the high-level selection of an algorithm to solve a given problem from a set of functionally equivalent algorithms. This section will give a overview of how the STAPL framework works as well as a brief summary of some performance results.

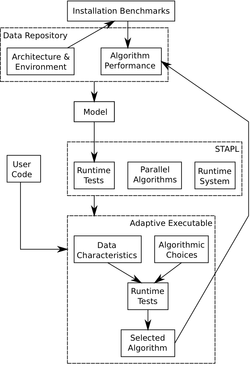
STAPL is, at it's core, a library of ISO Standard C++ components with interfaces similar to the regular ISO C++ standard library. It's underlying infrastructure consists of platform independent and platform dependent components. The core library consists of pAlgorithms (parallel algorithms, parallel equivalent of an STL algorithm) and pContainers (distributed data structures). STAPL programs can adapt to the underlying architecture through the use of a number of different algorithms that have the same interface and functionality but perform differently depending on the input data and underlying hardware. When STAPL is installed on a target system it collects information about the system from various standard header files and vendor system calls. Information regarding available memory, cache size, number of processors, etc. is gathered and stored in an internal data repository. At this point, a series of installation benchmarks for the algorithmic options available in STAPL are run and the resulting data is also stored in the data repository. The next step involves using machine learning techniques to analyze the data. Three different empirical learning approaches were implemented within the STAPL framework: a decision tree learner (used most often), a standard back propagation neural network and a naive Bayes classifier. All of the learners share a common input format and interface for querying for predictions, so they can be easily interchanged at any time. Once the prediction models are created they can be used, in conjunction with some small run-time tests, to predict which implementation of a given algorithm (with respect to a given input) should be used. These decisions are then monitored and fed back into the data repository so they can influence decisions made in the future. An overview of the STAPL framework is given in the figure provided.

One of the tests done on STAPL was on parallel sorting. In this test, they considered three popular yet very different parallel sorting algorithms: sample sort, radix sort and column sort. The details of each individual sorting algorithm are omitted here, but suffice to say that each one behaves very differently when the input and underlying hardware are varied. It was found that metrics such as the number of processors, cache size, number of elements in the input and the data type of these elements were important attributes of a given problem instance. Another metric that was also calculated at run-time was the degree of input presortedness, which can have a significant effect on the running time of the different sorting algorithms. All of this information was used by the learners to predict which algorithm to use. This test was done on three very different architectures and in all instances the decision tree prediction model performed best. Overall, STAPL was found to use the correct algorithm over 95% of the time on average. They also compared the adaptive solution provided by STAPL to a standalone version of the fastest algorithm for each input and found that the overhead incurred by STAPL was relatively small.

POET Transformation Engine

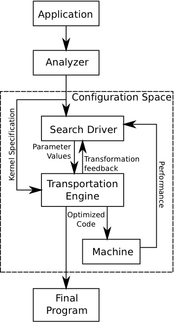
Yi et. al proposed a general purpose approach to high performance kernel optimization which relies on three main components: an analyzer, an empirical search driver and their specialized POET transformation engine [10]. Their system works in the following way. First, the analyzer looks at the application to be optimized and creates a kernel specification file which fully describes the computation in an abstract manner, allowing this system to be language independent. Currently these specifications are written manually for a given application, however it is expected that this process will be automated eventually by the creation of a special purpose optimizing compiler. Along with a complete description of the code to be optimized, this specification file also defines where and how to apply various optimization transformations that exist within the transformation engine. All of these aspects of the specification file are written in a small, special-purpose language named POET (Parameterized Optimizations for Empirical Tuning). Once the input specification is interpreted, the POET transformation engine builds an internal representation of the overall computation, including the areas of which can be tuned. From here an external search driver can be used to apply optimizations to the code that already exist within the POET TE, or the user has the opportunity to define and apply their own optimization strategies by encoding them in POET and incorporating them into the transformation engine. The empirical tuner applies various optimizations while also trying various parameter settings for these optimizations to achieve efficient code on a given architecture. These optimizations are tested and the results are fed back into the search driver to further improve performance. This process is summarized in the figure provided.

This system was then used to try and improve the performance of the ATLAS library discussed earlier on a few different architectures. To do this, relevant optimizations were implemented in the POET language and incorporated in the transformation engine. Next, specification files were hand written for each ATLAS kernel to be tuned. After tuning these various kernels, the POET tuned kernels were compared to the performance of the regular ATLAS kernels for both level 3 and level 2 BLAS operations. With respect to level 3 BLAS, POET performed relatively well against ATLAS, losing out on more than half of the comparisons but winning on others. In general, POET is at least competitive at this level. When it comes to the level 2 BLAS operations, the POET optimized kernels perform better than the ATLAS libraries in the majority of cases. In general, it is shown that the POET transformation engine can be used to improve performance critical applications (even those which are already highly optimized) in a relatively straight forward manner. One interesting note is that since none of the optimizations included in the transformation engine incorporate domain specific information about the ATLAS kernels, it is expected that the POET transformation engine can achieve similar levels of high performance for other scientific, performance-critical routines.

PetaBricks

Ansel et. al presented a new, implicitly parallel programming language and compiler which would allow for multiple implementations of an algorithm to solve a given problem and would ensure good performance on any given computer architecture. This language is called PetaBricks [1]. One of the main ideas behind this language was to expose algorithmic choice to the compiler. The language consists of two major constructs, transforms and rules. Transforms are similar to functions in that they define an algorithm. Rules are what make up a transform. Each rule defines how to compute a given region of the input data in order to make progress towards the final goal. Rules have well defined dependencies (ie. certain rules cannot be executed until other rules have). When a user calls a transform, they do not say how to apply it. It is the job of the compiler and run-time system to decide which rules to apply to complete the algorithm.

The RollingSum transform written in PetaBricks (reproduced from [1]).

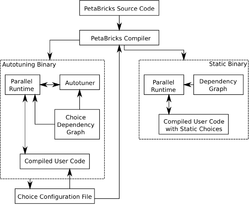
To understand how the PetaBricks compilation process works, consider the example code presented in the figure to the right. This code sample represents an implementation of the RollingSum transform. For a given input array A, we would like to compute an output array B where each element B[i] represents the sum A[0] + ... + A[i]. Rule 0 solves the output for a given element of B directly by adding up the appropriate values in A and rule 1 calculates a specific value in B by using the previous element of B and adding the appropriate value from A. Both of these rules calculate the correct output in different ways. Applying only rule 0 is slower (O(n^2)), but can be done in parallel where successive applications of rule 1 would be faster but must be done sequentially. This code will be compiled in the following way. First the code is parsed into an abstract syntax tree. Secondly, the rules would be analyzed to determine where each rule can be legally be applied to the input data. In the case of our example, rule 0 can be applied to any region of B, while rule 1 cannot be applied to the first position of B as it relies on the previous position to calculate its output. In the next step, a choice grid for each input type is constructed. A choice grid divides each input type (some kind of rectangular data structure) into rectangular regions where a uniform set of rules can be applied. From here, a choice dependency graph is constructed. The graph is constructed using the regions from the choice grid as vertices and edges representing data dependency. The choice dependency graph for our rolling sum example can be seen in the figure to the right where the dependency between rule 1 and rule 0 described above can be seen. Finally, code is generated using this graph. The code generation can be done in two ways. The default mode is to allow for algorithmic choice to be embedded in the output code which can be dynamically tuned later and then run with a configuration file describing the optimal choices. The second mode compiles code with a previously generated configuration file and hard codes the choices into the output code.

When an untuned binary is created using the process described above, it needs to be tuned on a specific architecture. To simplify this process, it is assumed that the optimal solution to a smaller sub-problem is independent of the larger problem that it comes from, which allows algorithms to be built starting with small inputs and working up to larger, more realistic sized inputs. The auto-tuner then builds multi-level algorithms where each level corresponds to a specific range of input sizes. The tuner then operates very much like a genetic tuner by first staring with a population of candidate algorithms. The input size is then raised and new levels consisting of different rules are added on top of the algorithms determined to be the most efficient in the previous round. The fastest algorithms move on while the slower ones are dropped. Since the algorithms from the previous steps are used as the base for algorithms at any given stage, optimal algorithms are built from the bottom up. The overall PetaBricks framework can be seen in the figure provided.

The paper included many example benchmarks, here we will briefly discuss the sorting transform implemented. For this problem, the following algorithms were implemented as rules within the sort transform: quick sort, n-way merge sort and a 16 bucket radix sort. Since all of these algorithms, except for insertion sort, are recursive, when a recursive call was made all of the algorithms would simply call the sort transform again instead of calling the specific algorithm (rule) in the recursive call. When the code was tuned on specific architectures, it built hybrid algorithms that would first use a 2-way merge sort, followed by quicksort, followed by insertion sort as the input sizes successively got smaller as the algorithm recursed. Surprisingly radix sort was never used. In general they found that their auto-tuned algorithms produced significant speedups compared to singe algorithm solutions.

Active Harmony and CHiLL

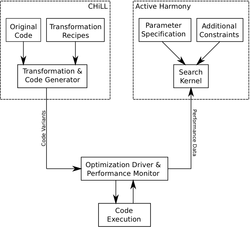
Finally, Tiwari et. al produced a general, scalable auto-tuning framework for compiler optimization [6]. Their system is comprised of two main components, Active Harmony and CHiLL. Active Harmony is an automated performance tuning infrastructure that provides algorithms to search for code parameter values to improve overall performance. An example use of active harmony is for finding a good set of loop transformation parameters, which represents the type of search that Active Harmony is designed to perform. CHiLL, on the other hand, is a code generation framework that allows for the rapid generation of different code variations. CHiLL allows for the composition of high-level loop transformations with a script interface used to describe the various transformations and the search space. This interface can be used to change parameters and receive output code quickly. A given algorithm can then tuned in the following way. First, the original code, along with possible code transformation recipes, are provided to the CHiLL compiler. The compiler then decomposes this information and stores it in a specialized internal representation of the overall computation. Parameters and constraints of the application at provided to Active Harmony, which then searches the optimization space. Active Harmony then requests a new code variation by supplying CHiLL with a set of parameters. This code variation is then run on the target architecture and the performance results are fed back into Active Harmony's search kernel. This process is repeated until a code variation of acceptable performance is produced. For an overview of this framework, see the figure provided.

To test the overall effectiveness of this framework, a matrix multiplication kernel and a triangular matrix problem solver were implemented to compare against ATLAS. At this point there were two versions of ATLAS available, the full version which had processor specific, hand-tuned assembly code included and the other didn't. For the matrix multiplication kernel, this framework performed on average 2.36 times faster than the native compiler and 1.66 times faster than the basic version of ATLAS. This code also ran within 20% of the processing time of the full version of ATLAS. For the triangular solver kernel, the generated code ran on average 3.62 times faster than the native compiled code and 1.07 time faster than the basic version of ATLAS. The full version of ATLAS, however, was 1.55 times faster. In general though this shows that their proposed framework can produce code that is significantly faster than natively compiled code and also able to compete with domain specific kernel libraries.

Conclusion

As the pace of hardware evolution continues to grow, the problem of portable, efficient code will grow as well. This will become a key challenge to the distributed computing community, who generally want to build very large systems made up of very diverse, heterogeneous parts. For these systems to be successful, they need to ensure that performance critical kernels will be efficiently implemented across their system to allow for the high level of performance expected from the user. The promise of auto-tuning algorithms has been realized for a small number of numerical problems, such as ATLAS for the BLAS problems. The main issue with these auto-tuners is that the optimizations they implement are generally domain specific and therefore difficult to generalize to other problems. Presented here was an overview of the emerging field of general purpose frameworks for performance-portable code. Although this area is relatively small, there are already some very mature frameworks which can allow for very versatile and efficient implementations of a wide range of algorithms. Although these systems all work slightly differently, they all strive for the same thing: the ability to allow the programmer to describe the algorithm they wish to implement in an abstract way to allow it to adapt to any given physical architecture. This, in turn, will result in an efficient implementation of a given algorithm anywhere. The overall importance of these frameworks will only grow as our computer architectures continue to evolve and become more complex.

References

[1] Jason Ansel, Cy Chan, Yee Lok Wong, Marek Olszewski, Qin Zhao, Alan Edelman, and Saman Amarasinghe. Petabricks: a language and compiler for algorithmic choice. In Proceedings of the 2009 ACM SIGPLAN conference on Programming language design and implementation, PLDI ’09, pages 38–49, New York, NY, USA, 2009. ACM. link

[2] Krste Asanovic, Ras Bodik, Bryan Christopher Catanzaro, Joseph James Gebis, Parry Husbands, Kurt Keutzer, David A. Patterson, William Lester Plishker, John Shalf, Samuel Webb Williams, and Katherine A. Yelick. The landscape of parallel computing research: A view from berkeley. Technical Report UCB/EECS-2006-183, EECS Department, University of California, Berkeley, Dec 2006. link

[3] Jee W. Choi, Amik Singh, and Richard W. Vuduc. Model-driven autotuning of sparse matrix-vector multiply on gpus. In Proceedings of the 15th ACM SIGPLAN symposium on Principles and practice of parallel programming, PPoPP ’10, pages 115–126, New York, NY, USA, 2010. ACM. link

[4] James Demmel, Jack Dongarra, Viktor Eijkhout, Erika Fuentes, Antoine Petitet, Richard Vuduc, R. Clint Whaley, and Katherine Yelick. Self-adapting linear algebra algorithms and software. Proc. IEEE, 93(2):293–312, February 2005. link

[5] John A. Gunnels, Fred G. Gustavson, Greg M. Henry, and Robert A. van de Geijn. Flame: Formal linear algebra methods environment. ACM Trans. Math. Softw., 27:422–455, December 2001.

[6] Justin Mazzola Paluska, Hubert Pham, Umar Saif, Grace Chau, Chris Terman, and Steve Ward. Structured decomposition of adaptive applications. In Proceedings of the 2008 Sixth Annual IEEE International Conference on Pervasive Computing and Communications, pages 1–10, Washington, DC, USA, 2008. IEEE Computer Society. link

[7] Nathan Thomas, Gabriel Tanase, Olga Tkachyshyn, Jack Perdue, Nancy M. Amato, and Lawrence Rauchwerger. A framework for adaptive algorithm selection in stapl. In Proceedings of the tenth ACM SIGPLAN symposium on Principles and practice of parallel programming, PPoPP ’05, pages 277–288, New York, NY, USA, 2005. ACM. link

[8] A. Tiwari, Chun Chen, J. Chame, M. Hall, and J.K. Hollingsworth. A scalable auto-tuning framework for compiler optimization. In Parallel Distributed Processing, 2009. IPDPS 2009. IEEE International Symposium on, pages 1 –12, May 2009. link

[9] Sundaresan Venkatasubramanian, Richard W. Vuduc. Tuned and wildly asynchronous stencil kernels for hybrid cpu/gpu systems. In Proceedings of the 23rd international conference on Supercomputing, ICS ’09, pages 244–255, New York, NY, USA, 2009. ACM. link

[10] Michael J. Voss and Rudolf Eigemann. High-level adaptive program optimization with adapt. SIGPLAN Not., 36:93–102, June 2001. link

[11] Clint Whaley, Antoine Petitet, and Jack J. Dongarra. Automated Empirical Optimization of Software and the ATLAS Project. Parallel Computing, 27, 2000. link

[12] Jianxin Xiong, Jeremy Johnson, Robert Johnson, and David Padua. Spl: a language and compiler for dsp algorithms. In Proceedings of the ACM SIGPLAN 2001 conference on Programming language design and implementation, PLDI ’01, pages 298–308, New York, NY, USA, 2001. ACM.

[13] Qing Yi and R. Clint Whaley. Automated transformation for performance-critical kernels. In Proceedings of the 2007 Symposium on Library-Centric Software Design, LCSD ’07, pages 109–119, New York, NY, USA, 2007. ACM. link