Introduction

The overall computer industry has changed drastically in the last 5-10 years. With multicore computing we no longer see the pattern of single chips with increasing clock speeds being released, we see the number of cores on a given chip increase as time goes on. In spite of this, Moore's law persists which lets us expect machines with hundreds if not thousands of individual cores in the not so distant future. Because of this we can also expect the physical makeup of individual machines to vary significantly and possibly be made up of heterogeneous smaller computational components. As described in the Berkeley View [2] this poses an enormous problem to the performance portability of code, as performance and portability are classically conflicting objectives when it comes to software generation. This is obviously a major concern in distributed computing as well since it is essential to have efficient code throughout the system, regardless of what physical architecture it resides on. For this reason, having code that can 'auto-tune' itself to achieve near optimal performance on any given hardware architecture will be a key issue moving forward within the distributed computing community and will be absolutely essential if the dream of a true distributed operating system running at internet scale is ever to be realized.

Many problems within the world of linear algebra have auto-tuned libraries which achieve near-optimal performance on a wide range of machines. One such system is ATLAS [9], which is presented here as an example. The problem with these libraries are that they are not general enough to service all of the high performance computing needs of the scientific community and the optimizations they employ are too specific to be applied to other problems. To combat this, a new area of general purpose frameworks for performance-portable code is emerging. The purpose of this literature review is to give the reader an overview of the most popular such frameworks that exist today, give an idea of how they work and briefly discuss their overall performance.

Motivation

The main motivation behind this work was presented in the The Landscape of Parallel Computing Research: A View from Berkeley [2]. This document discusses the recent switch of the computer hardware world to multicore processors and the drastic changes that need to be implemented in the software world to be able to adapt to the next generation of computers. The scope of this paper is much more than can be covered here, so the only important aspects that motivate our later discussion will be looked at.

Moore's law describes a trend in computer hardware where the number of transistors that could affordably be put on a chip doubled every 18 months to two years. In terms of processors, this would mean that one could expect faster and faster sequential computers to come out on a regular basis. This lead to the conventional wisdom that there was no real need for major optimizations or to parallelize sequential programs because they would simply run faster once a new generation of processors came out. However, due to many factors, the performance of individual processors have not been meeting the exponential improvements that they have in the past. In spite of this, Moore's law persists. Instead of seeing faster and faster individual cores, we now see the number of processor cores on a chip going up. It is currently not uncommon for a personal computer to have 2, 4 or even 8 processor cores. As this trend continues we can expect chips with thousands of individual cores on a single chip in the not so distant future. On top of this, it is not hard to imagine that the physical makeup of individual machines will vary significantly and possibly be made up of heterogeneous smaller computational components as well.

This obviously introduces some major problems into the world of computer software. Software vendors can no longer rely on faster individual cores to improve the performance of their sequential programs. Many already parallelized programs will not be able to scale as the number of cores increase dramatically, meaning they will effectively reach a performance barrier as well. Another equally, if not more urgent, problem is the issue of code performance portability. Currently, we write code and compile it to be efficient on a given machine. When this code needs to be run on a different machine, it is possible that significant changes must be made to the code and compilation process to get near optimal performance. Obviously this is undesirable as it demands a significant amount of time to adjust and tune the code by hand by highly trained experts. As the variety and complexity of heterogeneous systems increase, the time needed to hand tune code for specific machines becomes unmanageable. This is a key concern within distributed systems as overall performance is largely influenced by how quickly individual machines can execute code. If only a small number of machines have optimal code, then either the operating system will always try to use these machines for specific tasks, or it will run the tasks on machines with suboptimal implementations of the given code. Either way this results in poor overall performance.

One potential solution to these problems are new programming models and auto-tuning frameworks. Programming models need to allow the programmer to balance their productivity with implementation efficiently. One key way to do this is to abstract the underlying architecture from the programmer. This will allow the programmer to worry about implementing their program and leave the low level details to the system. However, regardless of the programming model used, the overall performance will be determined by the quality of the generated code, which is currently done by the compiler. The compiler is responsible for the optimization selection and then choosing the parameters for these optimizations as well as choosing between different alternative implementations of library kernels. This search space is often too large for a compiler to be able to make all of the right choices all of the time on every different computer architecture. Also, it is very difficult to add new optimizations into existing compilers and is often not worth the time needed to implement them. Because of this, most optimal solutions have to be manually tuned for each different system, taking a significant human investment. This is where auto-tuners step in. An auto-tuned algorithm is one that effectively searches through the optimization search space (either at compile time or run time) to produce efficient implementations on a wide array of hardware architectures. Auto-tuners have become popular in the last few years to produce highly portable, efficient scientific code. Many of these auto-tuners do this by generating many different algorithm variations of a given problem and then benchmark each one on a specific machine. The search also tries many combinations of the optimizations available through the compiler. This is a lengthy process, sometimes lasting several hours, but it only needs to be performed once at install time. The resulting implementation is often significantly faster than a naive implementations and sometimes even produces code faster than vendor supplied libraries. This is accomplished because the auto-tuner searches the optimization space in ways that a person would not, often finding unusual and unexpected optimization combinations. In the next section, an example of an auto-tuner implementing linear algebra libraries will be presented.

An Example of an Auto-tuned Algorithm: ATLAS

ATLAS (Automatically Tuned Linear Algebra Software) [9] is a software package that was produced to provide a portable and efficient implementation of the Basic Linear Algebra Subprograms (BLAS), a widely used linear algebra library. ATLAS is regarded as some of the earlier pioneering work in the field of auto-tuning algorithms, still being used by the scientific community as well as other researchers as a performance benchmark today.

BLAS are building block methods for performing basic linear vector and matrix operations. It has three logical levels. Below these levels are described as well as a brief summary of what ATLAS tries to do to make their code more efficient at each level.

Level 1 BLAS

This level performs vector-vector operations. At this level it is not possible to process the vectors to be able to reuse memory (as it is with matrix operations), and is expected to only achieve a roughly 0-15% speedup over untuned code. Generally the compiled can do a good job of optimizing this code so not many extra optimizations are performed by ATLAS.

Level 2 BLAS

This level performs matrix-vector operations. At this level using appropriate cache and register blocking can drastically reduce the references that must be satisfied out of main memory. By ensuring that certain segments of vectors and matrices remain in registers or in cache for a significant amount of time, one can expect a modest 10-300% speedup at this level.

Level 3 BLAS

This level performs matrix-matrix operations. Using major-block format for the matrices (with the correct size blocks) allows for a minimization of cache thrashing as well as maximizing the amount of cache that gets reused. Another important aspect of these operations is deciding on the order in which the matrices are computed in, especially if you are dealing with relatively small matrices. If not, a relatively complex partitioning of the matrices can ensure maximum memory reuse, which will in-turn produce significant performance improvements. A lot of significant details are being omitted here, but suffice to say that ATLAS achieves orders of magnitude of speedup at this level.

At install time ATLAS runs a series of benchmarks to calculate the various cache and main memory sizes as well as to determine various latency timings within the given system. ATLAS also probes the system to gain information regarding the floating point units of the system. On top of this, ATLAS explores other optimizations such as loop unrollings and blocking factors and applies the best ones found.

Although many of the details of ATLAS have been omitted here, it is hoped that this gives the reader an idea of what an auto-tuned algorithm tries to accomplish. Auto-tuning algorithms have been very successfully in the area of linear algebra (see [3, 4, 7] for other examples), however little has been done on non-numerical problems. One potential reason for this is the investment it takes to produce an efficient, portable auto-tuned algorithm. ATLAS and systems like it are certainly not trivial and are the result of many years of research and development. Another issue is that many other problems do not have the regular and pre-known data qualities that are common to many linear algebra problems. It is for these reasons that recently more general purpose approaches have taken off.

General Purpose Frameworks for Performance-Portable Code

As stated in the previous section, there has been a significant amount of work put in to auto-tuning algorithms related to linear algebra problems but not much work done outside of this. To combat this, some researchers looked at the problem of portable performance from another angle. Instead of focusing on a single problem and building an auto-tuned algorithm to solve that problem efficiently on a wide variety of computer architectures, we are starting to see the emergence of general purpose frameworks for performance-portable code. Generally speaking, these frameworks allow the programmer to define the problem that they are trying to solve without explicitly worrying about specific performance details. The framework would then have some kind of auto-tuner to then tune the code to allow for an efficient implementation on a given machine. Although this area is relatively small, there are already a handful of very powerful frameworks that allow for performance-portable code. In the following subsections an overview of the available frameworks will be given.

ADAPT

ADAPT [8] represents one of the earlier general purpose frameworks we will look at. It was realized that with the convergence of modern computing technology that it was possible to produce a single executable program for a wide range of compatible but still wildly varied computer systems. These differences can come from different memory sizes and hierarchies, processors and networking capabilities, all of which can have a significant impact on performance if not taken into consideration by the running program. To overcome this issue, Voss et. al proposed APAPT, a system that supports dynamic code compilation with parameterization while allowing the user to search the the optimization space to achieve near optimal performance.

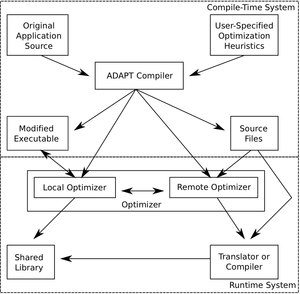
ADAPT has two main components, one being compile-time and the other being a run-time component. ADAPT provides its own language (ADAPT Language, or AL for short) for the users to define their optimization heuristics to be applied by the ADAPT run-time system. An example of an optimization heuristic written in AL was given in the paper, and it was for a dynamic loop unroller. Using this language it is possible to code a very wide range of optimization heuristics to help optimize the application code. The ADAPT compiler reads the application code as well as user-defined optimization heuristics and generates a run-time system for applying these these heuristics dynamically to the application. To do this, the compiler first identifies code pieces that are candidates for optimization. The compiler then generates a run-time system based on the candidate code sections as well as the user supplied optimization heuristics. This run-time system consists of the original application code with new control paths for each optimization candidate. For each candidate, the first path represents the best known version of the code (using whatever optimizations have been applied in the past) and the second path represents an experimental version. Every time a new experimental version is created, it is run at the next opportunity (the next time that piece of code is called). The experimental version is monitored and then its performance data is fed back into the optimizer. This allows the ADAPT optimizer to successively swap in better and better performing pieces of code and represents a key component of the overall ADAPT framework.

The ADAPT optimizer consists of two parts, a local optimizer as well as a remote optimizer. The local optimizer identifies hotspots within the code, representing the most time consuming sections. The local optimizer will then communicate this information to the remote optimizer which has the source code of each candidate, a description of the target machine, the user specified optimization heuristics and tools and compilers that can be used to optimize the code. The remote optimizer then optimizes the code with all of the tools it has available to it and when a new code variant is produced, it is sent back to the local optimizer to be dynamically linked into the running application to be run and evaluated at the next opportunity. The more that a section candidate code is run, the faster it gets over time due to this process. ADAPT relies on this fact to achieve peak performance in its applications. An overview of the ADAPT framework can be seen provided figure.

The ADAPT framework was then tested on two different computer systems by running six different experiments. These experiments covered different applications, including floating point benchmarks, kernels for matrix-matrix multiplication and a finite differencing solver. These experiments give an idea of the variety of techniques that can be implemented using the ADAPT framework. It was found that, on average, the ADAPT system offers a better solution than static optimization tools. In general, ADAPT was found to offer the best performance with the least risk of degradation in all of the tests performed.

References

[1] Jason Ansel, Cy Chan, Yee Lok Wong, Marek Olszewski, Qin Zhao, Alan Edelman, and Saman Amarasinghe. Petabricks: a language and compiler for algorithmic choice. In Proceedings of the 2009 ACM SIGPLAN conference on Programming language design and implementation, PLDI ’09, pages 38–49, New York, NY, USA, 2009. ACM.

[2] Krste Asanovic, Ras Bodik, Bryan Christopher Catanzaro, Joseph James Gebis, Parry Husbands, Kurt Keutzer, David A. Patterson, William Lester Plishker, John Shalf, Samuel Webb Williams, and Katherine A. Yelick. The landscape of parallel computing research: A view from berkeley. Technical Report UCB/EECS-2006-183, EECS Department, University of California, Berkeley, Dec 2006.

[3] Jee W. Choi, Amik Singh, and Richard W. Vuduc. Model-driven autotuning of sparse matrix-vector multiply on gpus. In Proceedings of the 15th ACM SIGPLAN symposium on Principles and practice of parallel programming, PPoPP ’10, pages 115–126, New York, NY, USA, 2010. ACM.

[4] James Demmel, Jack Dongarra, Viktor Eijkhout, Erika Fuentes, Antoine Petitet, Richard Vuduc, R. Clint Whaley, and Katherine Yelick. Self-adapting linear algebra algorithms and software. Proc. IEEE, 93(2):293–312, February 2005.

[5] Nathan Thomas, Gabriel Tanase, Olga Tkachyshyn, Jack Perdue, Nancy M. Amato, and Lawrence Rauchwerger. A framework for adaptive algorithm selection in stapl. In Proceedings of the tenth ACM SIGPLAN symposium on Principles and practice of parallel programming, PPoPP ’05, pages 277–288, New York, NY, USA, 2005. ACM.

[6] A. Tiwari, Chun Chen, J. Chame, M. Hall, and J.K. Hollingsworth. A scalable auto-tuning framework for compiler optimization. In Parallel Distributed Processing, 2009. IPDPS 2009. IEEE International Symposium on, pages 1 –12, May 2009.

[7] Sundaresan Venkatasubramanian, Richard W. Vuduc. Tuned and wildly asynchronous stencil kernels for hybrid cpu/gpu systems. In Proceedings of the 23rd international conference on Supercomputing, ICS ’09, pages 244–255, New York, NY, USA, 2009. ACM.

[8] Michael J. Voss and Rudolf Eigemann. High-level adaptive program optimization with adapt. SIGPLAN Not., 36:93–102, June 2001.

[9] Clint Whaley, Antoine Petitet, and Jack J. Dongarra. Automated Empirical Optimization of Software and the ATLAS Project. Parallel Computing, 27, 2000.

[10] Qing Yi and R. Clint Whaley. Automated transformation for performance-critical kernels. In Proceedings of the 2007 Symposium on Library-Centric Software Design, LCSD ’07, pages 109–119, New York, NY, USA, 2007. ACM.